题目一:中国台湾初中数学竞赛题目,若$a+b=12$,求$\sqrt{a^2+4}+\sqrt{b^2+49}$的最小值。
解题思路:类似题目,如果代入求取最小值,难度较大,可以换一种思维方式,用数形结合的方法求解,不仅容易理解而且简洁明了。
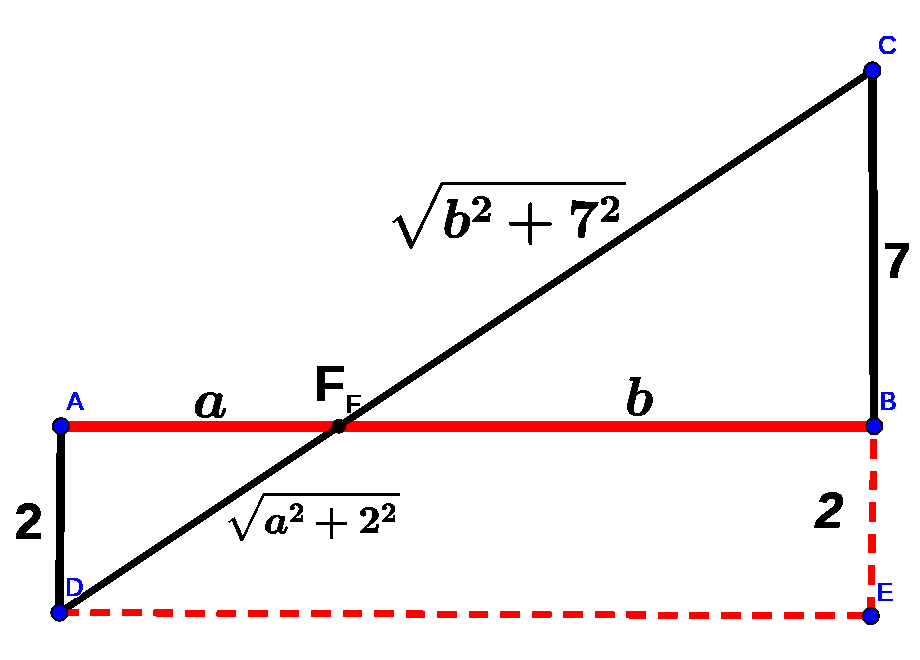
线段$AB=12,AF=a,BF=b$,过B点作AB的垂直线段$BC=7$,过A点作AB的垂直线段AD=2,连接CF、DF,则$\triangle CBF和\triangle DAF$都是直角三角形,根据勾股定理可得:$CF=\sqrt{b^2+7^2},DF=\sqrt{a^2+2^2}$,两点之间线段最短!显然当线段CF、DF在同一条直线上时CD的值是最小的。过D点作AB的平行线,与BC延长线交于E点。
$\begin{split}\text{解:}\\&\because a+b=12\Rightarrow AB=DE=12,CE=BC+BE=9\\&\therefore\text{根据勾股定理可得:}(CD)^2=(CE)^2+(DE)^2\\&\therefore CD=\sqrt{a^2+2^2}+\sqrt{b^2+7^2}=\sqrt{(CE)^2+(DE)^2}=\sqrt{{12}^2+9^2}=15\\\\&\therefore\text{数形结合有的时候是解决代数式最大值、最小值问题的法宝,简洁明了,尤其适合填空题和选择题!}\end{split}$
题目二:$\begin{split}&\triangle ABC中,AB=CD,\\&\angle ABD=40^{\circ},\angle BAD=30^{\circ},\end{split}$求$\angle\alpha=\angle ACD=?$,奥数竞赛几何题目,如果没有想到巧妙的辅助线,做起来比较难。
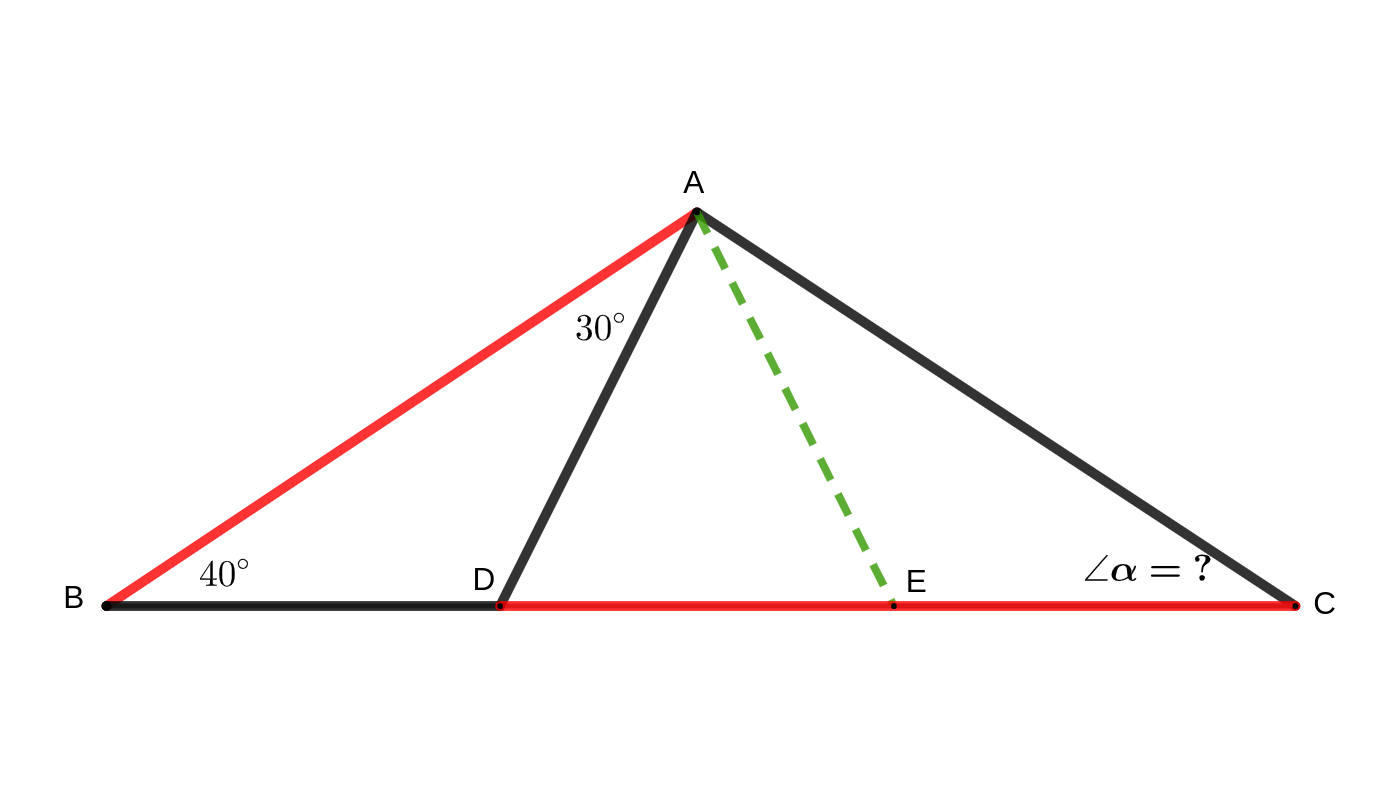
$\begin{split}\text{解:}\\&作辅助线,在BC上取一点E,连接AE,使得:BA=BE,\triangle ABE是等腰三角形\\&\therefore AB=BE,\angle AED=70^{\circ},\angle DAE=40^{\circ}\Rightarrow \angle ADE=70^{\circ},\triangle ADE也是等腰三角形\\&\Rightarrow AE=AD\\&\because AB=BE=CD\\&\therefore BD=BE-DE=AB-DE=CD-DE=CE\\&\Rightarrow BD=CE,\angle ADB=\angle AEC=180^{\circ}-70^{\circ}=110^{\circ}\\&\therefore \triangle ABD\cong\triangle ACE\\&\therefore \angle\alpha=\angle ACE=\angle ABD=40^{\circ}\end{split}$
拓展思维题:俄罗斯的初中数学竞赛题目,有些猛。求:$\bbox[yellow,5pt,border:2px solid red]{\cos18^{\circ}\sin36^{\circ}}$的值。
解题思路:$\sin18^{\circ}$的值可以使用数形结合的方式求解,既然$\sin18^{\circ}$可以求解,那么$\cos18^{\circ}$也可以求解。同样,$\sin36^{\circ}$也可以用数型结合的方式进行计算。总之,如果只用初中知识求解,计算量较大,化简起来需要一定的变换技巧,这个$\sin18^{\circ}$的求值方法在初中数学竞赛中常见,一般来说,就是数形结合求值最简洁。
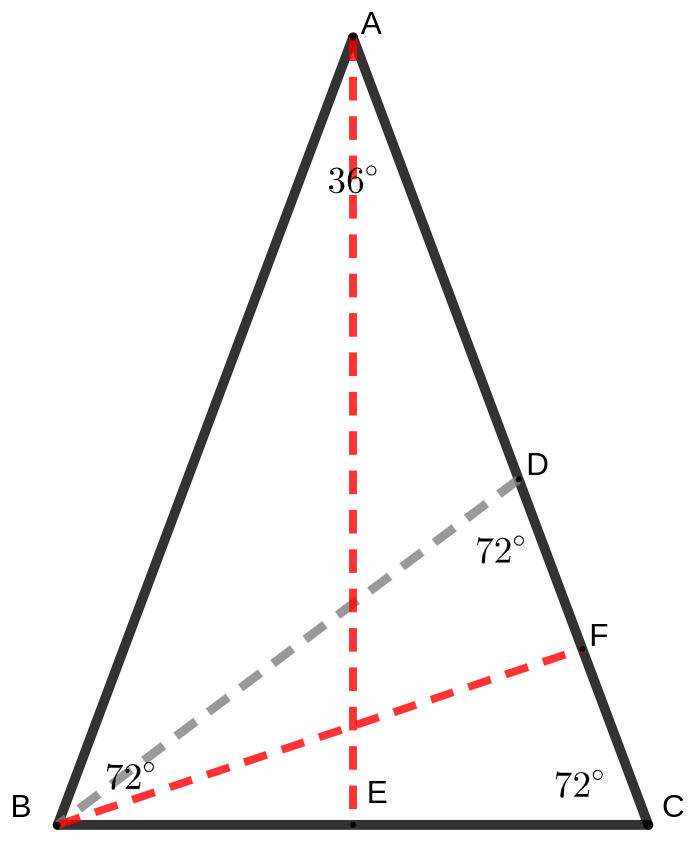
$\begin{split}\text{解:}\\&初中解法:作一个等腰三角形\triangle ABC,顶角为\angle BAC=36^{\circ},两个底角为\angle ABC=\angle ACB=72^{\circ};\\&过B点作\angle ABC的角平分线交边AC于D点,过A点作底边AC的高交于E点。\\&过B点作边AC的高交于F点\\&\therefore \triangle DAB和 \triangle BCD也是等腰三角形:设AD=BD=BC=1,DC=m\\&\because \triangle ABC\backsim\triangle BCD\Rightarrow \dfrac{AC}{BC}=\dfrac{BC}{DC}=\dfrac{BD}{DC}\Rightarrow \dfrac{1+m}{1}=\dfrac{1}{m}\\&\therefore m^2+m-1=0\Rightarrow m=\dfrac{-1\pm\sqrt5}{2}\\&\text{负数根舍去:}m=\dfrac{\sqrt5-1}{2}\Rightarrow AB=AC=\dfrac{\sqrt5+1}{2}\\&\text{根据几何关系及三角函数定义:}\\&\sin18^{\circ}=\dfrac{CE}{AC}=\dfrac{\dfrac12\cdot BC}{AD+DC}=\dfrac{\dfrac12}{1+\dfrac{\sqrt5-1}{2}}=\dfrac{\sqrt5-1}{4}\\&\because \sin^2\alpha+\cos^2\alpha=1\\&\therefore \cos18^{\circ}=\sqrt{1-\sin^218^{\circ}}=\sqrt{\dfrac{5+\sqrt5}{8}}\\&\because S_\triangle ABC=AC\cdot BF=BC\cdot AE\Rightarrow \dfrac{\sqrt5+1}{2}\cdot BF=1\cdot AE\\&AE=\sqrt{(AC)^2-(\dfrac12\cdot BC)^2}=\sqrt{\Big(\dfrac{\sqrt5+1}{2}\Big)^2-\dfrac14}=\sqrt{\dfrac{5+2\sqrt5}{4}}\\&\therefore BF=\dfrac{\sqrt{5+2\sqrt5}}{\sqrt5+1}\\&\therefore \sin36^{\circ}=\dfrac{BF}{AB}=\dfrac{2\sqrt{5+2\sqrt5}}{(\sqrt5+1)^2}\\&\therefore \cos18^{\circ}\sin36^{\circ}=\dfrac{\sqrt{5+2\sqrt5}\cdot\sqrt{5+\sqrt5}}{\sqrt2\cdot(\sqrt5+1)^2}=\dfrac{\sqrt{35+15\sqrt5}}{\sqrt2(6+2\sqrt5)}\\&=\dfrac{\sqrt5\sqrt{7+3\sqrt5}}{2\sqrt2(3+\sqrt5)}=\dfrac{\sqrt5\sqrt{\dfrac12\cdot \left(9+6\sqrt{5}+5\right)}}{2\sqrt2(3+\sqrt5)}=\dfrac{\sqrt5\sqrt{{\dfrac12}\cdot\left(3+\sqrt5\right)^2}}{2\sqrt2(3+\sqrt5)}=\dfrac{\sqrt5}{4}\\&\therefore \bbox[yellow,5pt,border:2px solid red]{\text{用初中知识求解,计算量还是比较大的,尤其最后一步,俄罗斯竞赛题目挺生猛!}}\\&\text{如果用高中数学知识求解,难度降低不少:}\\&\because \sin2\alpha=2\sin\dfrac{\alpha}{2}\cdot\cos\dfrac{\alpha}{2},\sin^2\alpha+\cos^2\alpha=1\\&\therefore \sin36^{\circ}=2\sin18^{\circ}\cos18^{\circ}\\&\therefore \cos18^{\circ}\sin36^{\circ}=2\sin18^{\circ}\cdot\cos^2{18}^{\circ}=2\sin18^{\circ}\cdot(1-\sin^2{18}^{\circ})\\&=2\cdot\dfrac{\sqrt5-1}{4}\cdot(1-\dfrac{6-2\sqrt5}{16})=\dfrac{\sqrt5}{4}\\&\bbox[yellow,6pt,border:2px solid red]{\text{用高中的三角函数公式求解,难度降低很多,不用化简复杂根式了!}}\end{split}$
题目三:罗马尼亚奥林匹克初中数学竞赛题,已知$a、b、c\in\mathbb Z,abc\ne0,a\ne c,\dfrac a c=\dfrac{a^2+b^2}{c^2+b^2}$,证明:$a^2+b^2+c^2\text{不是质数。}$
解题思路:类似的数论方面的题目,倒是在数学竞赛中常见,需要比较严谨的思路,对质数的性质需要熟练掌握,有一定难度。这道题目用到的拓展三角不等式是一个不常见的考点,容易被忽略。
$\begin{split}\text{解:}\\&\because \dfrac a c=\dfrac{a^2+b^2}{c^2+b^2}\Rightarrow a(c^2+b^2)=c(a^2+b^2)\\&\Rightarrow ab^2-cb^2+ac^2-ca^2=0\Rightarrow b^2(a-c)+ac(c-a)=0\\&\therefore (a-c)(b^2-ac)=0\\&\because a\ne c\Rightarrow a-c\ne0\\&\therefore b^2-ac=0\Rightarrow b^2=ac\\&\therefore a^2+b^2+c^2=a^2+2ac+c^2+b^2-2ac=(a+c)^2-b^2=(a+c+b)(a+c-b)\\&\therefore a、b、c\in\mathbb Z,abc\ne0,a\ne c\bbox[yellow,5pt,border:2px solid red]{\Rightarrow a^2+b^2+c^2=\vert a+c+b\vert\cdot\vert a+c-b\vert\gt0}\\&\therefore \vert a\vert、\vert c\vert\text{不可能都是$1$,至少有一个}\geqslant2\\&\therefore a^2+b^2+c^2\gt\vert a\vert+\vert b\vert+\vert c\vert\\&\bbox[yellow,5pt,border:2px solid red]{\text{由三角不等式:}\vert x\vert+\vert y\vert+\vert z\vert\geqslant\vert x\pm y\pm z\vert}\\&\therefore a^2+b^2+c^2\gt\vert a\vert+\vert b\vert+\vert c\vert\geqslant\vert a+c\pm b\vert\\&\therefore a^2+b^2+c^2\gt\vert a+c+b\vert且 a^2+b^2+c^2\gt\vert a+c-b\vert\\&\because a^2+b^2+c^2\text{可以分解成为两个小于其本身的两个数的乘积} \\&\therefore\text{根据质数的性质,} a^2+b^2+c^2\text{不可能是质数!}\\\\&\bbox[yellow,6pt,border:2px solid blue]{\text{从这道题目的难度来看,罗马尼亚孩子的数学水平真是挺高的!}}\end{split}$
题目四:法国初中数学竞赛题,解方程:$\sqrt{3+\sqrt{9+x}}=\sqrt[3]{x}$
解题思路:乍一看,方程左边是根号,右边是开三次方,去根号似乎是一个不错的选择,但是仔细一看,比较复杂,计算量太大,不行!只能使用换元法去根号。
$\begin{split}\text{解:}\\&\because \sqrt{9+x}\geqslant0\Rightarrow \sqrt{3+\sqrt{9+x}}\geqslant\sqrt{3}\gt1\\&\therefore \sqrt[3]{x}\gt1\\&令\sqrt[3]{x}=a(a\gt1)\Rightarrow x=a^3\\&\sqrt{3+\sqrt{9+x}}=a\Rightarrow 3+\sqrt{9+x}=a^2\Rightarrow \sqrt{9+x}=a^2-3\\&\text{方程两边平方去根号可得:}9+x=a^4+9-6a^2\text{将$x=a^3$代入可得:}\\&a^4-a^3-6a^2=0\Rightarrow a^2(a^2-a-6)=0\\&\because a\gt1\Rightarrow a^2\gt1\\&\therefore a^2-a-6=0\Rightarrow (a-3)(a+2)=0\\&\therefore a=3(a=-2不符合题意,故舍去)\\&\therefore x=a^3=3^3=27\\\\&\bbox[yellow,6pt,border:3px solid red]{\boldsymbol{\text{类似换元法需要熟练掌握,法国孩子的数学水平跟美国孩子差不多!}}}\end{split}$
题目五:江苏省初中数学竞赛题,已知$a、b\in\Bbb R$,且$\dfrac4{a^4}-\dfrac2{a^2}=5,b^4+b^2=5$,求$\dfrac4{a^4}+b^4$的值。
解题思路:观察发现,两个条件似乎十分相似,可以使用一种特殊的方式进行换元,然后通过韦达定理转换后求解,这种思路倒是十分巧妙。
$\begin{split}\text{解:}\\&\dfrac4{a^4}-\dfrac2{a^2}=5\Rightarrow \left(-\dfrac2{a^2}\right)^2+\left(-\dfrac2{a^2}\right)-5=0\\&b^4+b^2=5\Rightarrow \Big(b^2\Big)^2+b^2-5=0\\&\text{令$x_1=-\dfrac2{a^2},x_2=b^2$}\\&\therefore x_{1,2}是方程:x^2+x-5=0的两个根!根据韦达定理:\\&x_1+x_2=-1,x_1\cdot x_2=-5\\&\therefore\dfrac4{a^4}+b^4=(x_1)^2+(x_2)^2=(x_1+x_2)^2-2x_1\cdot x_2=(-1)^2-2\times(-5)=11\\\\&\bbox[yellow,6pt,border:2px solid red]{\text{如此看来,中国孩子的数学水平的确比国外孩子的水平高多了。}} \end{split}$
题目六:北京市六中自主招生题,解方程:$x^2-4x-2=\dfrac{3}{x-3}+\dfrac{5}{x-5}$
解题思路:如果直接化简,出现四次方,无法求根。只能设法使用换元法求解了,观察发现,方程的左边有$x-4$,方程的右边有$x-3,x-5$,这种情况下,通常使用均值换元法。
$\begin{split}\text{解:}\\&\text{原方程可以变形为:}x^2-4x=\dfrac{3}{x-3}+1+\dfrac{5}{x-5}+1=\dfrac{x}{x-3}+\dfrac{x}{x-5}\\&\Rightarrow x\Bigg[(x-4)-\left(\dfrac{1}{x-3}+\dfrac{1}{x-5}\right)\Bigg]=0\\&\therefore x_1=0或者\left(x-4\right)-\left(\dfrac{1}{x-3}+\dfrac{1}{x-5}\right)=0\\&\text{使用均值换元法,令$t=x-4$则:}\\&t-\Big(\dfrac{1}{t+1}+\dfrac{1}{t-1}\Big)=0\Rightarrow t-\dfrac{2t}{t^2-1}=0\Rightarrow t\Big(1-\dfrac{2}{t^2-1}\Big)=0\\&\therefore t=0\Rightarrow x-4=0\Rightarrow x_2=4\\&\text{或者$1-\dfrac{2}{t^2-1}=0$}\Rightarrow t^2-1=2\Rightarrow t^2=3\Rightarrow t=\pm\sqrt{3}\\&\Rightarrow x-4=\pm\sqrt{3}\Rightarrow x_{3,4}=4\pm\sqrt{3}\\&\therefore\bbox[yellow,6pt,border:2px solid red]{ x_1=0,x_2=4,x_3=4+\sqrt3,x_4=4-\sqrt3}\end{split}$
