你从来没有对这些现象好奇过吗?
为什么三角形三条中线过同一点?
为什么三角形三条高线过同一点?
为什么三角形三条角平分线过同一点?
为什么三角形垂直平分线过同一点?
这就需要用到两个著名的定理,梅涅劳斯定理和塞瓦定理。在平面几何中,这两个定理的地位可以说举足轻重,应用广泛。
梅涅劳斯定理(Menelaus’ theorem)
梅涅劳斯(Menelaus,公元98年左右),是希腊数学家和天文学家,大约生活在我国东汉年间。梅涅劳斯定理是平面几何中的一个重要定理,这个定理很早就被证明过了。
过三角形一边上的点做一直线,分别与其余两边或其延长线所截,则满足一下关系:
$\displaystyle \frac{AF}{FB}\cdot\frac{BD}{DC}\cdot\frac{CE}{EA}=1$

塞瓦定理(Ceva’s theorem)
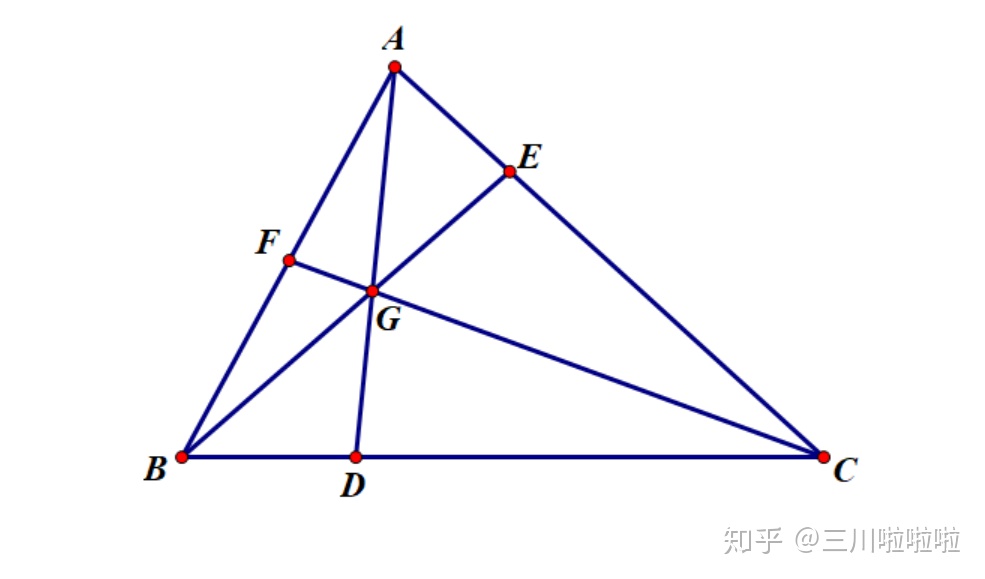
塞瓦(G·Ceva,1647-1734)是意大利的数学家和水利工程师,他在1678年(我国清朝康熙17年)发表了一个著名的定理,后世以他的名字来命名,叫做塞瓦定理。连结三角形一个顶点和对边上一点的线段叫做这个三角形的一条塞瓦线。
三角形内三线交于一点,则有以下关系:
$\displaystyle \frac{AF}{FB}\cdot\frac{BD}{DC}\cdot\frac{CE}{EA}=1$
实际上这两个定理互为「对偶定理」,即只要证明其中一个,另一个自然成立。这是因为在射影平面中,确定一条直线和确定一个点,都需要三个坐标(齐次坐标),于是面空间与点空间形成了自然的同构,而这样的同构映射保持结合性不变,所谓结合性,就是指「点在线上」、「线过某点」这样的结合关系。
对偶图形包含两个方面:
1.图元素互换:「点」与「线」互换;
2.结合性互换:「共点」与「共线」互换。
它们俩的逆定理也是成立的,这根据三角形的唯一性可以得到。
这两个定理的证明并不复杂,只需要初中的几何知识足以证明这两个定理。令人费解的是,这两个定理被证明的时间居然跨越了1500多年,也许是后来的数学大咖们觉得塞瓦定理就是梅涅劳斯定理的一个等价变换无需再次证明吧?互联网上可以找到各种证明方法,在此不赘述。
我国的数学工作者张景中院士在《新概念几何》中利用「共边定理」证明「梅涅劳斯定理」和「塞瓦定理」的方法独树一帜,非常简洁,证明长度均为一行,而且引理本身也是足够简明直观,现简单介绍如下:
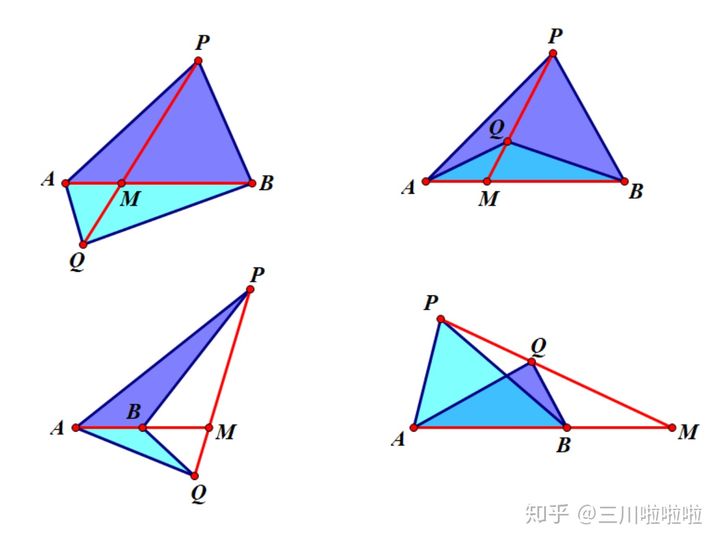
共边定理:两个三角形共用一条边(AB),连接非共边的顶点(P点和Q点),与共边或者其延长线相交于M点,则有:
$\displaystyle \frac{S_{\triangle PAB}}{S_{\triangle QAB}}=\frac{PM}{QM}$。
该定理有四种情况(参见左边的几何图形示例,当然PM与PA或者PB重合时可视为其中一种情况的特例)
关于共边定理,可以通过两个共边三角形面积之比等于两个高之比以及相似三角形对应边成比例的定理轻松证明,初中几何知识足够,这里不再赘述。最精彩的证明开始了,根据上面的三角形共边定理,可以轻松证明梅涅劳斯定理和塞瓦定理,证明过程就一行,非常简洁:
梅涅劳斯定理证明:
$\displaystyle \frac{AF}{FB}\cdot\frac{BD}{DC}\cdot\frac{CE}{EA}=\frac{S_{\triangle AED}}{S_{\triangle BED}}\cdot\frac{S_{\triangle BED}}{S_{\triangle CED}}\cdot\frac{S_{\triangle CED}}{S_{\triangle AED}}=1$

塞瓦定理证明:
$\displaystyle \frac{AF}{FB}\cdot\frac{BD}{DC}\cdot\frac{CE}{EA}=\frac{S_{\triangle GCA}}{S_{\triangle GBC}}\cdot\frac{S_{\triangle GAB}}{S_{\triangle GCA}}\cdot\frac{S_{\triangle GBC}}{S_{\triangle GAB}}=1$

